Volúmen
Es el espacio que ocupa un cuerpo
Los cuerpos geométricos existen en el espacio y son por lo tanto objetos que tienen tres dimensiones (ancho, alto y largo) limitados por una o más superficies. Si todas las superficies son planas y de contorno poligonal, el cuerpo es un poliedro. Si el cuerpo no está limitado por polígonos, sino por superficies curvadas recibe el nombre de cuerpos redondos.
La fórmula para calcular el volumen de un cuerpo depende de su forma.
Para medir el volumen de un cuerpo se utilizan unidades cúbicas, que son: milímetro cúbico, centímetro cúbico, decímetro cúbico y metro cúbico.
Definición
Un Sólido o Cuerpo Geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa un lugar en el espacio y en consecuencia tiene un volumen.
Los cuerpos geométricos tridimensionales ocupan siempre un espacio. La medida de ese espacio recibe el nombre de volumen. Asimismo, los cuerpos que están huecos pueden albergar en su interior otros cuerpos (sólidos, líquidos o gaseosos) en una cantidad que recibe el nombre de capacidad.
Cuando estudiamos las áreas hablábamos de dos dimensiones: largo y ancho. El producto de los valores largo X ancho nos da el área.
Para calcular un volumen necesitamos tres dimensiones: largo, ancho y alto. El producto de los valores largo X ancho X alto nos da el volumen.
Es lo mismo que decir, el volumen lo calculamos también multiplicando el área de la base por la altura.
Según el Sistema Internacional de Unidades, el volumen es representado por el metro cúbico. En la vida cotidiana el litro también puede ser considerado como una unidad del volumen. Además este sistema permite catalogar al volumen en tres clases.
En primer lugar pueden ser mencionadas las unidades de capacidad. Este tipo de unidades son utilizadas para calcular el espacio que ocupan las cosechas que se hayan almacenadas, por ejemplo gracias a ella se calcula el volumen de papas, zanahorias, manzanas, etc. Si bien este sistema ya ha sido remplazado por nuevas tecnologías, en la antigüedad resultaba una práctica corriente ya que no existían otros métodos más adecuados.
En segundo lugar pueden ser mencionadas las unidades de volumen en estado líquido. Este tipo de unidades se utilizan para calcular el espacio que ocupan los líquidos cuando se encuentran en un recipiente. La unidad elemental es en este caso el decímetro cúbico.
En tercer y último lugar se pueden mencionar las unidades de volumen en estado sólido. En este caso el volumen es calculado por medio de unidades que son elevadas a la tercera potencia. Estas serán siempre unidades de longitud. Esta es una práctica muy utilizada en la disciplina de la geometría y es de allí de donde proviene su nombre. En este caso el metro cúbico es la unidad elemental. Uno de sus múltiplos es el kilómetro cúbico, mientras que uno de sus submúltiplos es el centímetro cúbico.
Volúmenes de doble curvatura
Los volúmenes de revolución son volúmenes de doble curvatura, engendrados por una generatriz curva, que gira alrededor de un eje.
Si se secciona el cono en posiciones diferentes en el espacio, dichas secciones producen las llamadas curvas cónicas, que son la base generatriz de las superficies de revolución.
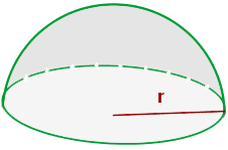
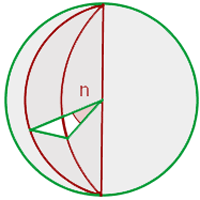
La esfera es el volumen regular por excelencia, producto del giro de un circulo en su diámetro
El esferoide identifica el volumen cuya superficie es el producto de girar una elipse alrededor de uno de sus ejes principales.
Las parábolas y las hipérbolas dan lugar a una rica variedad de superficies curvas.
Un paraboloide de revolución, es el volumen cuya superficie es generada por la rotación de una parábola alrededor de su eje de simetría
El hiperboloide de revolución, es el volúmen cuya superficie es generada por la rotación de una hipérbola alrededor de su eje de simetría
El interés topológico del paraboloide hiperbólico, conocido también como silla de montar, radica en que combina del mismo lado de su superficie, concavidad y convexidad.
Los paraboloides hiperbólicos incorporan en su geometría parábolas e hipérbolas.
El toro anular es una de los volúmenes de revolución topológicamente más importantes, producto del desplazamiento de un círculo a lo largo de unatrayectoria circular.






































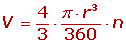






No hay comentarios.:
Publicar un comentario