Superficies

• Una superficie es el lugar geométrico de las posiciones distintas de una línea o curva en el espacio. 
• Una superficie es la envoltura que circunda a un cuerpo. Los planos directores o directrices son los que establecen el movimiento de la generatrices de la superficie. 
• Pueden ser limitadas o ilimitadas según que contengan un volumen finito dentro de un cuerpo o no. 
• Superficie tangencial es aquella que tiene una línea común como otra superficie, sin cortarla ni atravesarla.
• Superficie plana es aquella en la que se pueden trazar líneas rectas en cualquier dirección de la misma.
• Superficie envolvente es la que genera distintas posiciones de otra superficie llamada involuta.

Tipos de Superficies

Regladas 

Superficie generada por el movimiento de una recta, denominada generatriz, manteniéndose en contacto con otra u otras líneas, denominadas directrices, cumpliendo además en su desplazamiento ciertas condiciones particulares.

Alabeadas

Es una superficie reglada nó desarrollable, es decir, en la cual, dos posiciones sucesivas de la generatriz no son coplanares. Entre este tipo de superficies, se puede citar:

cilindroide: la generatriz (g) se desplaza manteniéndose paralela a un plano director (d) y apoyada sobre dos directrices (d1 y d2) curvas,

conoide: la generatriz (g) se desplaza manteniéndose paralela a un plano director (d) y apoyada sobre dos directrices, siendo una de ellas recta (d1) y la otra curva (d2).

Superficie doblemente reglada: Superficie alabeada en la cual por cada uno de sus puntos pasan dos generatrices (g1 y g2). Entre ellas se pueden citar:

paraboloide hiperbólico: la generatriz (g) se desplaza manteniéndose paralela a un plano director (d) y apoyada sobre dos directrices rectas (d1 y d2) que se cruzan,

hiperboloide de revolución: la generatriz (g) se apoya sobre dos directrices (d1 y d2) circulares, paralelas, y se mueve manteniendo constante el ángulo (a0) que forma ellas.

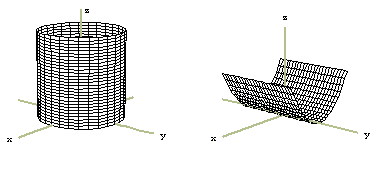
Simple curvatura

Superficie reglada en la cual cada dos posiciones adyacentes de la generatriz (g) son coplanares (son paralelas o se cortan).

Las superficies de curvatura simple son superficies desarrollables, es decir, pueden extenderse sobre un plano. Ejemplos de estas superficies son:

superficie cilindrica: superficie generada por el movimiento de una generatriz (g) que se mantiene en contacto con una directriz (d) curva, siendo además paralelas todas las posiciones de la generatriz; se clasifican en:

superficie cilindrica de revolución: superficie cilíndrica en la cual todas las posiciones de la generatriz (g) equidistan de un eje (e), paralelo a ella,

superficie cilindrica de nó revolución: superficie cilíndrica en la cual no es posible definir un eje (e) que equidiste de todas las posiciones de la generatriz (g),

superficie cónica: superficie reglada generada por el movimiento de una generatriz (g), manteniéndose en contacto con una directriz (d) curva, teniendo, todas las posiciones de la generatriz (g), un punto común (V), denominado vértice; se clasifican en:

superficie cónica de revolución: superficie cónica en la cual, todas las posiciones de la generatriz (g), forman el mismo ángulo con un eje (e), que pasa por el vértice (V),

superficie cónica de nó revolución: superficie cónica en la cual no es posible definir un eje (e), que forme el mismo ángulo con todas las posiciones de la generatriz.

Superficie cilíndrica

Es aquella que genera una recta cuando se mueve siempre paralela a una dirección dada.

Doble curvatura

Son superficies generadas por el movimiento de una generatriz (g) curva. Estas superficies no contienen líneas rectas y por lo tanto no son desarrollables. Entre ellas son muy conocidas las cuádricas, las cuales son superficies generadas por la rotación de una curva cónica alrededor de uno de sus ejes. Las cuádricas son:

esfera: la generatriz (g) es una circunferencia,

elipsoide: la generatriz (g) es una elipse,

paraboloide: la generatriz (g) es una parábola,

hiperboloide: La generatriz (g) es una hipérbola.

Superficies radiadas :

Son las que se generan por el movimiento de una recta apoyada en un punto propio o impropio y sobre una línea o curva.Las superficies radiadas son regladas (eso quiere decir que si tomamos una generatriz de la misma podemos seguir toda su superficie con el canto de una regla) y desarrollables (se pueden extender sobre un plano) además pueden ser cilíndricas o prismáticas si el punto de contacto con la regla está en el infinito.

Superficie cónica

Se engendra por una línea recta que se desplaza incidiendo siempre en un mismo punto fijo y por una línea directriz curva. (Línea directriz es aquella línea por la que pasan todas las generatrices, y las generatrices son las líneas que determinan la superficie).

La superficie es reglada por estar formada por cilindros (intersección de 3 cilindros iguales de ejes concurrentes ortogonales). Los cilindros son superficies cuyas generatrices pueden seguirse con una regla tocando todos sus puntos.

Superficies desarrollables

Son las que se pueden extender sobre un plano sin deformación, como por ejemplo las superficies cilíndricas y cónicas. Dos generatrices infinitamente próximas se cortan. Si un plano es tangente a la superficie en un punto lo es en toda la generatriz que pasa por ese punto,por regla general cualquiera de estas propiedades son suficientes para que la superficie sea considerada desarrollable.

Superficies cerradas

Un ejemplo de una superficie cerrada y múltiplemente conexa es el triple toro.

Intuitivamente una superficie cerrada en el espacio tridimensional es cualquier superficie que encierra un volumen, dividiendo a dicho espacio en una región "acotada" y una región "no acotada". En 4 o más dimensiones también existen superficies cerradas pero la noción intuitiva anterior no es válida, ya que las superficies cerradas en más dimensiones no dividen al espacio de esta forma.

Superficie compuesta

Es aquella engendrada o constituida por la combinación de otras.

Superficie de revolución

Está engendrada por una línea o curva que gira en torno a un eje y es co-planaria con él.

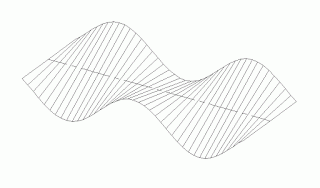
Superficies de evolución

Como refiere su nombre, son superficies que evolucionan con curvas o líneas de distinta forma. Superficie de evolución es aquella que evoluciona o se transforma, generándose por la unión de curvas distintas. En la figura un cuadrado se transforma de forma uniforme en una circunferencia. Para su construcción digital se utiliza el comando solevación. Su apariencia a veces es de una forma imposible, de una figura con una perspectiva mal dibujada -como la que aparenta el dibujo.

Como ejemplo de superficies de evolución o de desarrollo tenemos carrocerías de automóviles, fuselajes de aviones, casco de navíos y superficies irregulares complejas que suelen ser redondeadas y suaves y cuya definición del contorno no es suficiente para definirlas. La forma de definirlas es mediante proyecciones principales o secciones principales entre planos paralelos. Es algo análogo a lo que se hace en el sistema acotado, representar una montaña por líneas de contorno o de nivel, este es un ejemplo también del método que se viene haciendo desde hace años para la construcción de barcos.

Superficie poliédrica

Es la que está constituida por varios planos que se cortan entre sí.

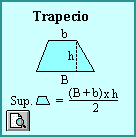
Cálculo de Superficies

Los polígonos son equivalentes cuando tienen la misma superficie, aunque tengan distinta forma. Esta propiedad es de suma utilidad para calcular la superficie de diferentes polígonos.

Construcción

Construcción de polígonos mediante el compás.

Mediante la aplicación de los conceptos referentes a los ángulos de los polígonos, es posible servirse del instrumento de dibujo que es el compás, para construir graficamente diversos polígonos.

El compás es un instrumento básicamente aplicable en el trazado de circunferencias, que delimitan una figura plana que es el círculo; el cual puede ser considerado un tipo especial de polígono regular, en el cual todos sus lados están constituídos solamente por un punto, y cuya dimensión está determinada por la longitud del radio, que es equivalente a la abertura del compás.

El método a utilizar para construir polígonos mediante el uso del compás, se basa en determinar los vértices de los lados del polígono, estableciendo en qué puntos de la circunsferencia deben situarse para que el polígono resulte inscripto en ella.

Esa determinación se realiza a partir del conocimiento de los valores de los ángulos centrales del polígono que se desea construir.

Para trazar un triángulo equilátero inscripto en un círculo, manteniendo el radio (abertura del compás) empleado para trazar el círculo, se determina un punto de la circunferencia (preferiblemente en la vertical inferior de su centro), y centrando en ese punto se traza un arco con extremos en la circunsferencia.

Los puntos de intersección (A y B) determinan un lado del triángulo equilátero; por lo cual tomando la medida de ese segmento con el compás y trasladándola sobre la parte superior de la circunferencia, se determinará el vértice (C) de unión de los otros dos lados.

Para trazar un cuadrado inscripto en un círculo, se traza una recta que pasando por el centro llegue a la circunsferencia en sus extremos (diámetro AB).

Con una abertura del compás mayor a la empleada para trazar el círculo, centrando en los puntos extremos del diámetro, se marcan puntos en la circunferencia; lo que determinará dos nuevos puntos (C y D). Uniéndolos mediante una recta, resultará un nuevo diámetro perpendicular al anterior; cuyos puntos de contacto con la circunferencia serán los vértices del cuadrado inscripto.

Como el cuadrado inscripto queda en posición transversal, puede trazarse otro con los lados en posición horizontal y vertical, simplemente trazando las medianas del cuadrado anterior, para determinar los vértices A', B', C' y D', de un nuevo cuadrado inscripto en el mismo círculo.

Para trazar un hexágono inscripto en un círculo, se fija un punto sobre la circunferencia, y con la misma abertura del compás, se marcan puntos haciendo centro primero en ese punto y luego sucesivamente en los nuevos puntos.

Ello determinará que se marquen sobre la circunferencia los seis puntos que corresponden a los vértices del hexágono.